Session-based Recommendation with Graph Neural Networks
Technical Highlights
We propose a novel method Session-based Recommendation with Graph Neural Networks (SR-GNN) composed of:
Modeling session graphs
Learning node representations
Generating session representations
Making recommendation
Extensive experiments conducted on real datasets show that SR-GNN evidently outperforms SOTA methods consistently.
Session-based Recommendation
Modern recommender systems help users find relevant items of interest. Most academic research is concerned with approaches that personalize the recommendations according to long-term user profiles. In many real-world applications, however, such long-term profiles often do not exist and recommendations therefore have to be made solely based on the observations of a user with the system during an ongoing session.
An example of session-based recommendation:
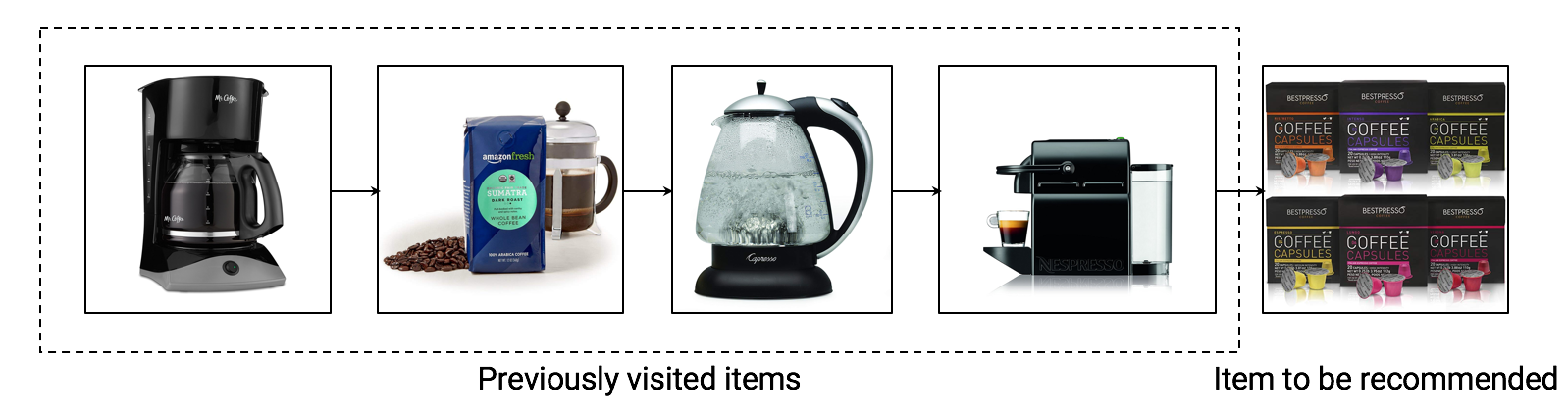
Assume a user has visited the above five items in a e-commerce website consecutively. The first four will be used as the training data and our goal is to accurately predict the last item. It is not necessary for the user to log into the system and other auxiliary information may not be available as well.
Challenges
We identify two main challenges for the session-based recommendation problem:
- Previous work reveals that complex user behavioral patterns are of great significance for session-based recommendation. How to effectively capture the item transitions in session sequences is one main obstacle to session-based recommendation.
- To facilitate recommendation, how to obtain accurate item embeddings and session embeddings is another key issue.
Revisiting Graph Neural Networks
Graph Neural Networks (GNNs)
- Proposed in [Scarselli et al. 2009]
- Propagation: computes representation for each node.
- Output mapping: maps from node representations and corresponding labels to an output.
- Model training via Almeida-Pineda algorithm
Gated Graph Neural Networks (GGNNs)
- Proposed in [Li et al. 2016]
- Uses gated recurrent units.
- Unrolls the recurrence for a fixed number of steps.
- Computes gradients through Backpropagation through time.
GNNs and GGNNs are graph-based neural networks, whose purpose is both to compute representation for each node. The only difference is GGNN introduces gated recurrent units and unrolls the recurrence for a fixed number of steps.
The Proposed Method
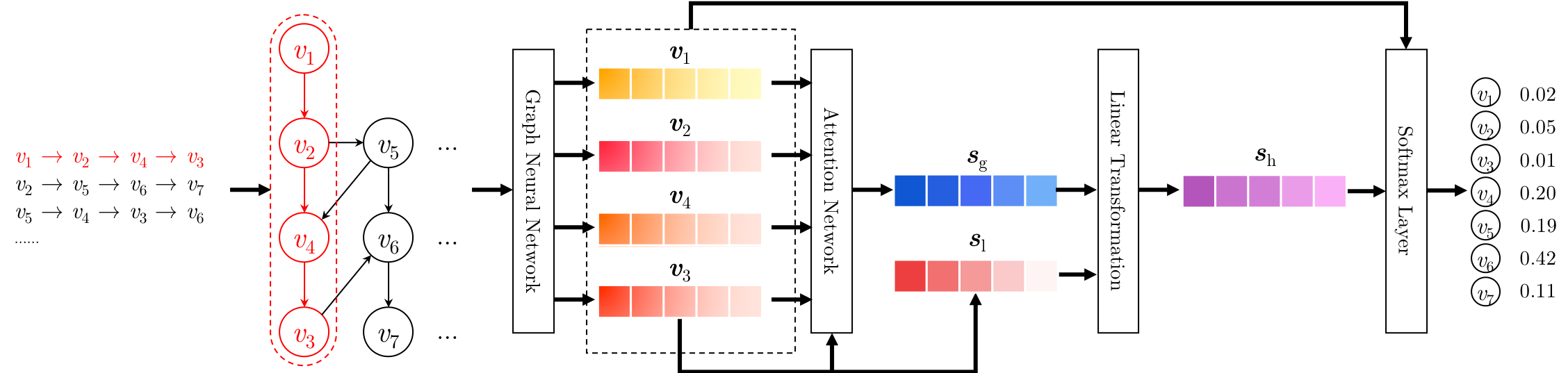
The proposed SR-GNN consists of the following four steps:
- Session graph modeling
- Node representation learning
- Session representation generating
- Making recommendation
Constructing Session Graphs
Each session sequence $s$ is modeled as a directed graph $\mathcal{G}_s = (\mathcal{V}_s, \mathcal{E}_s)$. We also conduct edge weight normalization: the occurrence of the edge divided by the outdegree of that edge’s start node.
While it is true that other types of neural networks, such as recurrent neural networks, can also learn the temporal dynamics of users’ interactions with items, there are some particular advantages to using graph structures for this task.
Firstly, the graph structure can be seen as representing the users’ underlying intentions and preferences, and the users’ interactions with items can be seen as samples drawn from this intention distribution. By learning the intention distribution, the recommender system can make more accurate and personalized recommendations by taking into account not only the users’ interests, but also their habits and preferences. For example, if a user frequently visits a certain category of items, such as sports news articles, and then transitions to a related category, such as sports equipment, the recommender system can use this information to suggest sports equipment products that are likely to be of interest to the user.
Another advantage of using graph structures is that they can be more efficient and scalable than other types of neural networks. Because graph neural networks are designed to operate on graph-structured data, they can exploit the inherent sparsity and regularity of the data to reduce the computational complexity of the model. This can make it easier to train large and complex graphs, such as those that arise in session-based recommendation, where the number of items and transitions can be very large.
Learning Item Embeddings on Graphs
We adopt GGNNs for learning unified representations for all nodes in session graphs.
The main propagation rules:
\[\begin{align} \boldsymbol{a}^t_{s,i} & = \boldsymbol{A}_{s,i:} \left[\boldsymbol{v}^{t-1}_1, \dots ,\boldsymbol{v}^{t-1}_n\right]^\top \boldsymbol{H} + \boldsymbol{b}, \\ \boldsymbol{z}^t_{s,i} & = \sigma\left(\boldsymbol{W}_z\boldsymbol{a}^t_{s,i}+\boldsymbol{U}_z\boldsymbol{v}^{t-1}_{i}\right), \\ \boldsymbol{r}^t_{s,i} & = \sigma\left(\boldsymbol{W}_r\boldsymbol{a}^t_{s,i}+\boldsymbol{U}_r\boldsymbol{v}^{t-1}_{i}\right), \\ \widetilde{\boldsymbol{v}^t_{i}} & = \tanh\left(\boldsymbol{W}_o \boldsymbol{a}^t_{s,i}+\boldsymbol{U}_o \left(\boldsymbol{r}^t_{s,i} \odot \boldsymbol{v}^{t-1}_{i}\right)\right), \\ \boldsymbol{v}^t_{i} & = \left(1-\boldsymbol{z}^t_{s,i} \right) \odot \boldsymbol{v}^{t-1}_{i} + \boldsymbol{z}^t_{s,i} \odot \widetilde{\boldsymbol{v}^t_{i}} . \end{align}\]The first equation aggregates information from neighbors specified by a connection matrix. The remaining equations are GRU-like updates.
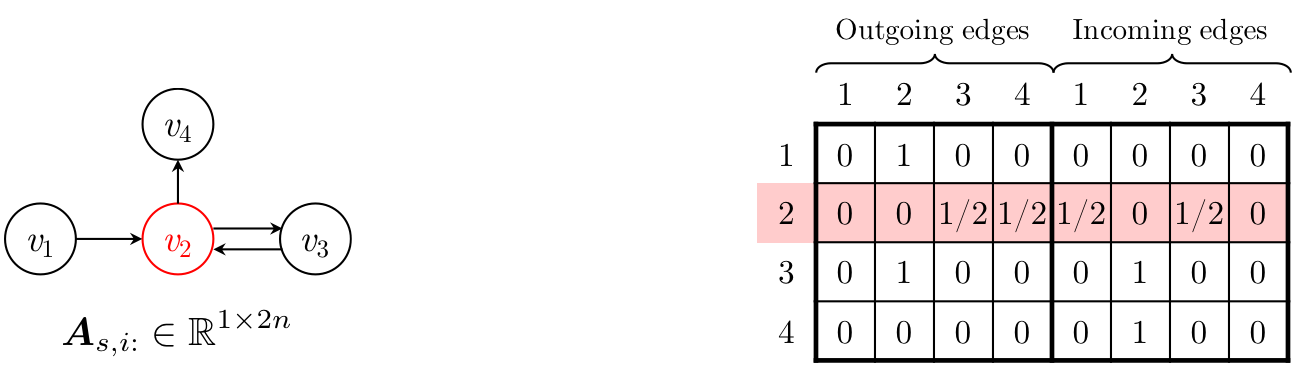
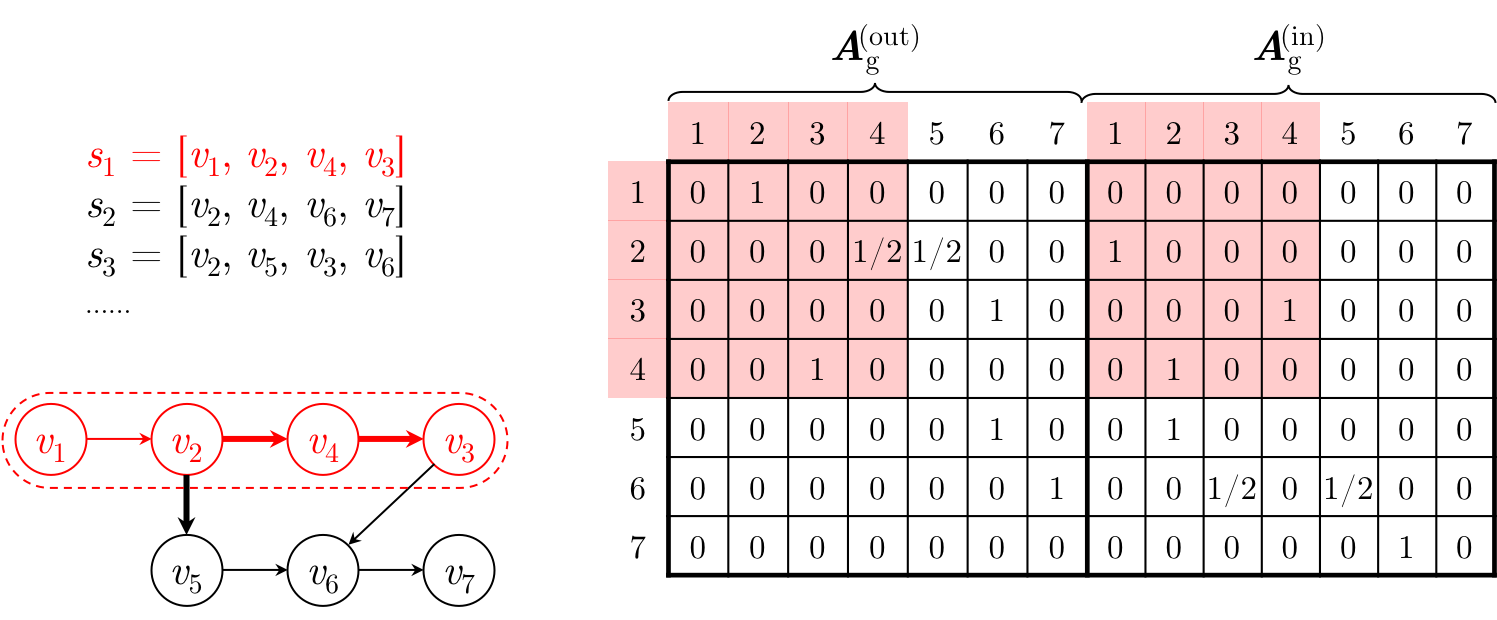
The connection matrix $\boldsymbol{A}_s \in \mathbb{R}^{n \times 2n}$ determines how nodes within the graph communicate with each other, which is defined as a concatenation of two adjacency matrices $\boldsymbol{A}_s^{\text{(out)}}$ and $\boldsymbol{A}_s^{\text{(in)}}$. $\boldsymbol{A}_{s,i:}$ are the two columns of blocks corresponding to node $v_{s,i}$.
Generating Session Embeddings
After obtained item embeddings, we generate session embeddings. A session is represented directly by node embedding involved in that session.
At first, we represent the user’s current interest aka., the local embedding to emphasize the impact of the last clicked item.
\[\boldsymbol{s}_\text{l} = \boldsymbol{v}_{n}\]While, the global embedding is obtained via a soft-attention network to represent the global preference. $q$, $\boldsymbol{W}_1$, and $\boldsymbol{W}_2$ control the weights.
\[\begin{align} \alpha_i & = \boldsymbol{q}^\top \, \sigma(\boldsymbol{W}_1 \boldsymbol{v}_{n} + \boldsymbol{W}_2 \boldsymbol{v}_{i} + \boldsymbol{c}), \\ \boldsymbol{s}_\text{g} & = \sum\limits_{i = 1}^{n} {\alpha_i \boldsymbol{v}_{i}}. \end{align}\]Then, we combine the two vectors through a simple linear transformation to get the hybrid embedding.
\[\boldsymbol{s}_\text{h} = \boldsymbol{W}_3 \left[\boldsymbol{s}_\text{l}; \boldsymbol{s}_\text{g}\right]\]Making Recommendation
Finally, we compute the score for each candidate item by multiplying its embedding by its session representation. Then, we apply a softmax function to get the output vector of the model.
\[\hat{\boldsymbol{y}} = \operatorname{softmax}\left( \boldsymbol{s}_\text{h}^\top \, \boldsymbol{v}_i \right)\]For each session graph, the loss function is defined as the cross-entropy of the prediction and the ground truth.
\[\mathcal{L}(\hat{\boldsymbol{y}}) = -\sum_{i = 1}^{m} \boldsymbol{y}_i \log{(\hat{\boldsymbol{y}_i})} + (1 - \boldsymbol{y}_i) \log{(1 - \hat{\boldsymbol{y}_i})}\]Experiments
Datasets
Baselines
- POP and S-POP
- Item-KNN [Sarwar et al. 2001]
- BPR-MF [Rendle et al. 2009]
- FPMC [Rendle et al. 2010]
- GRU4REC [Hidasi et al. 2016]
- NARM [Li et al. 2017a]
- STAMP [Liu et al. 2018]
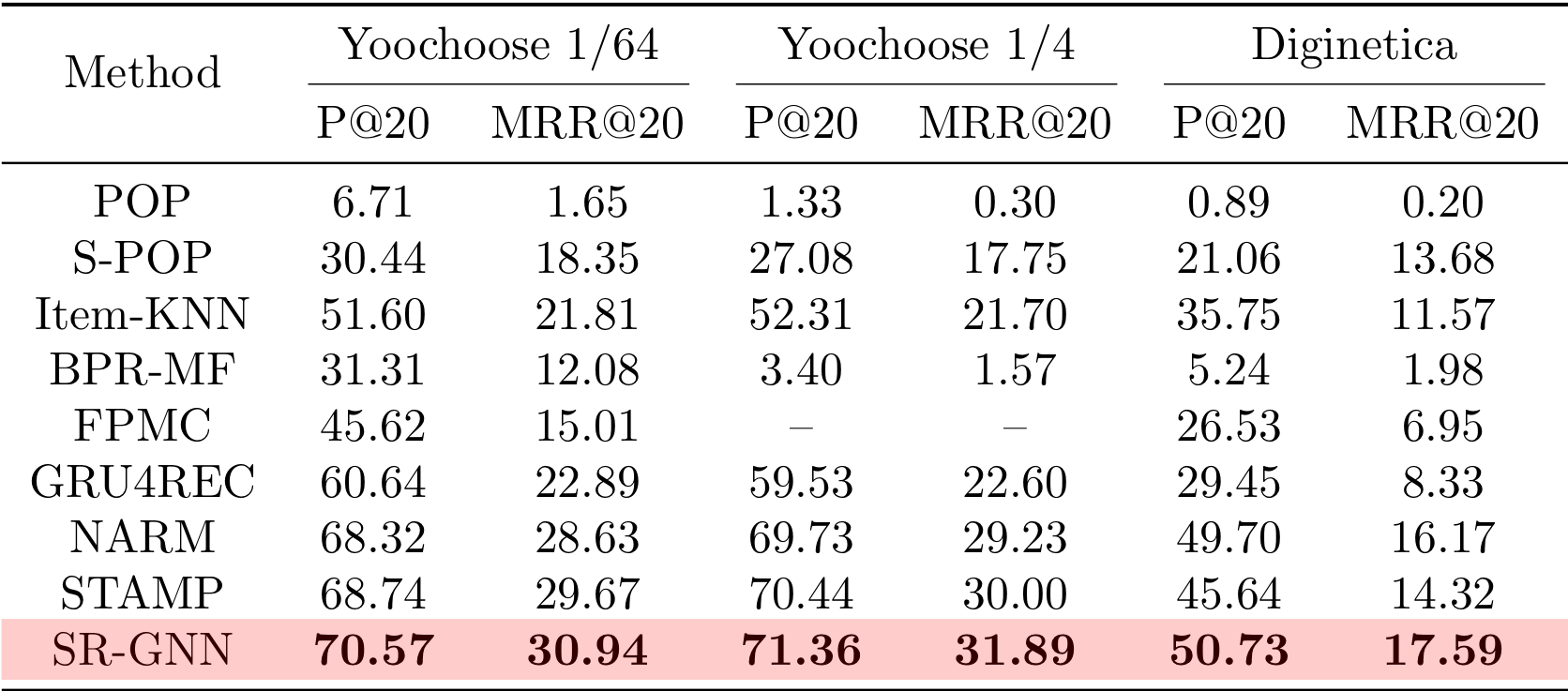
Comparison with Baselines
Variants of Connection Schemes
Our method is flexible in different recommendation scenarios. Considering user behavior in sessions is limited, we here propose two connection schemes to augment relationships between items in each session graph.
-
SR-GNN with normalized global connections (SR-GNN-NGC) replaces the connection matrix with edge weights extracted from the global graph on the basis of SR-GNN.
-
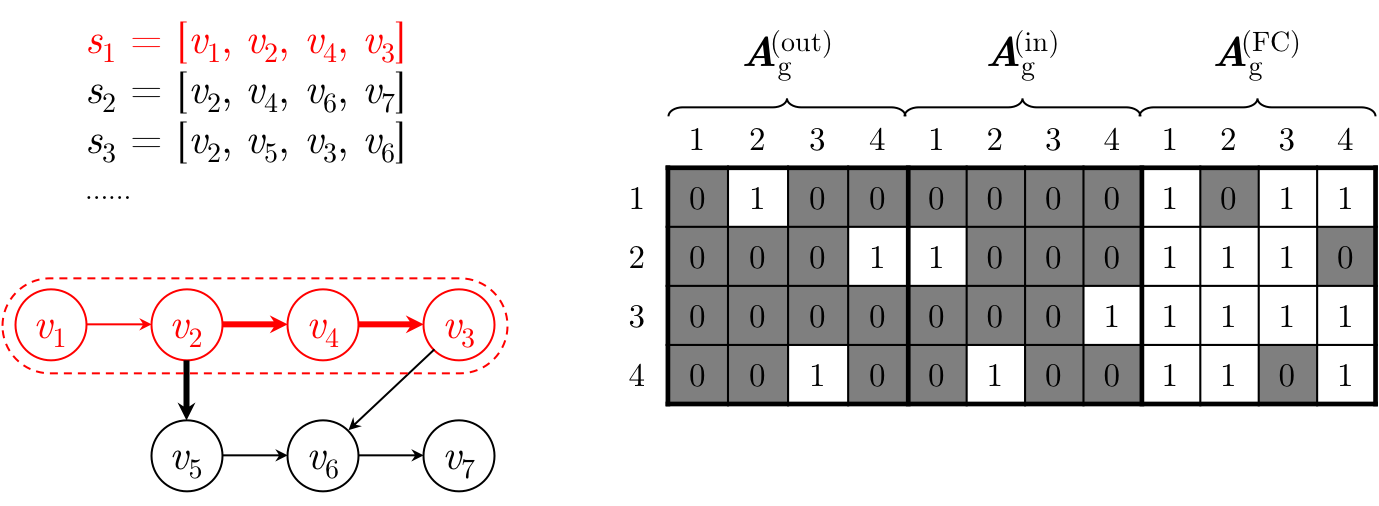
SR-GNN with full connections (SR-GNN-FC) represents all higher-order relationships using boolean weights and appends its corresponding connection matrix to that of SR-GNN.
Compared with SR-GNN, SR-GNN-NGC reduces the influence of edges that are connected to nodes. Such a fusion method notably affects the integrity of the current session, especially when the weight of the edge in the graph varies, leading to performance downgrade.
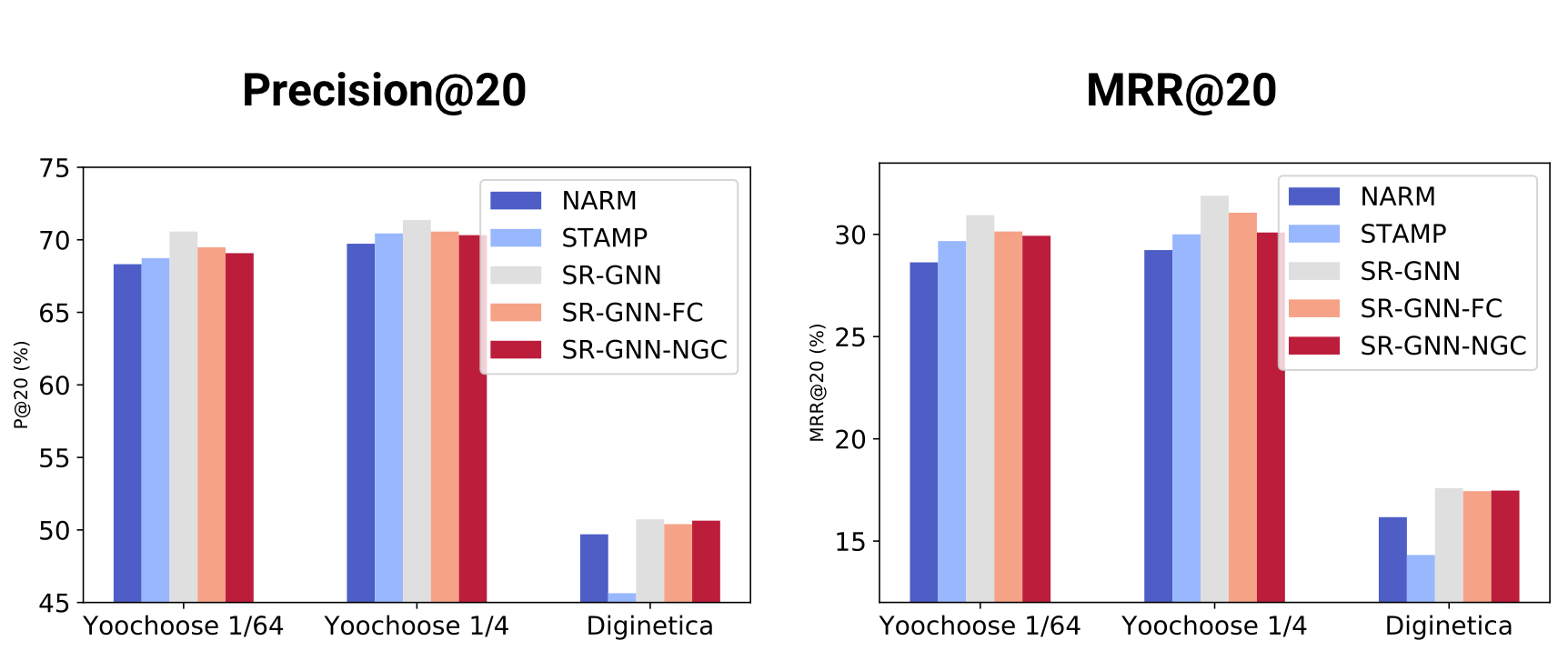
Similarly, it is reported that SR-GNN-FC performs worse than SR-GNN, though the experimental results of the two methods are not of many differences. Such a small difference suggests that in most recommendation scenarios, not every high-order transitions can be directly converted to straight connections and intermediate stages between high-order items are still necessities.
Variants of Session Representations
We then conduct ablation studies on the session representations:
- SR-GNN-L: local embedding only
- SR-GNN-AVG: global embedding with average pooling
- SR-GNN-ATT: global embedding with attention networks
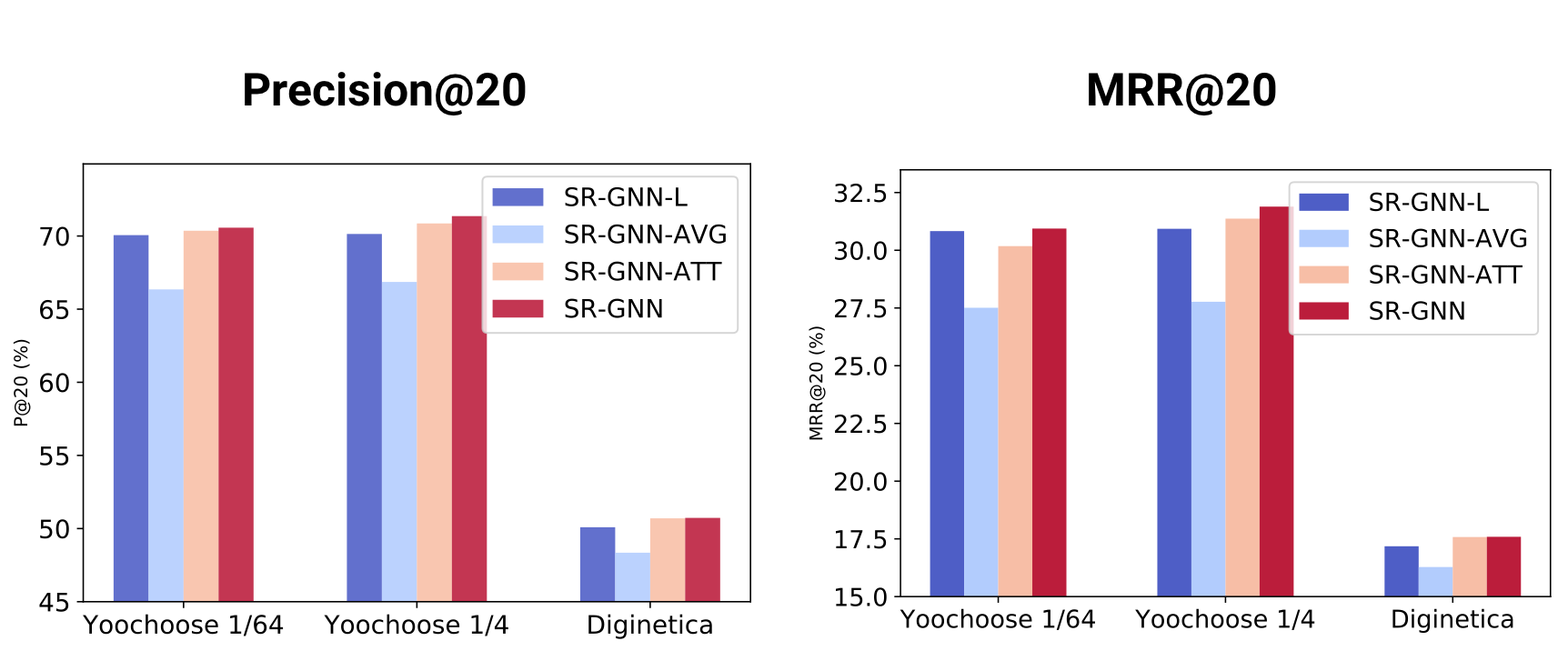
It can be observed that the hybrid embedding method SR-GNN yields best results on all three datasets. It validates the importance of explicitly incorporating current session interests with the long-term preference.
Furthermore, the figures show that SR-GNN-ATT performs better than SR-GNN-AVG with average pooling, which indicates that the session may contain some noisy behavior, which cannot be treated independently. Besides, it is shown that attention mechanisms are helpful in extracting the significant behavior from the session data to construct the long-term preference.
Please note that SR-GNN-L, a downgraded version of SR-GNN, still outperforms SR-GNN-AVG and achieves almost the same performance as that of SR-GNN-ATT, supporting that both the current interest and long-term preference are crucial for session-based recommendation.
Comparison of Sequence Lengths
Finally, we split the dataset into two groups such that we may observe the result brought with different sequence lengths. The pivot point is chosen according to the average length of session sequences.
- Short group: session lengths ≤ 5
- Long group: session lengths > 5
Our proposed SR-GNN perform stably on two datasets with different session lengths. It demonstrates the superior performance of the proposed method and the adaptability of graph neural networks in session-based recommendation.
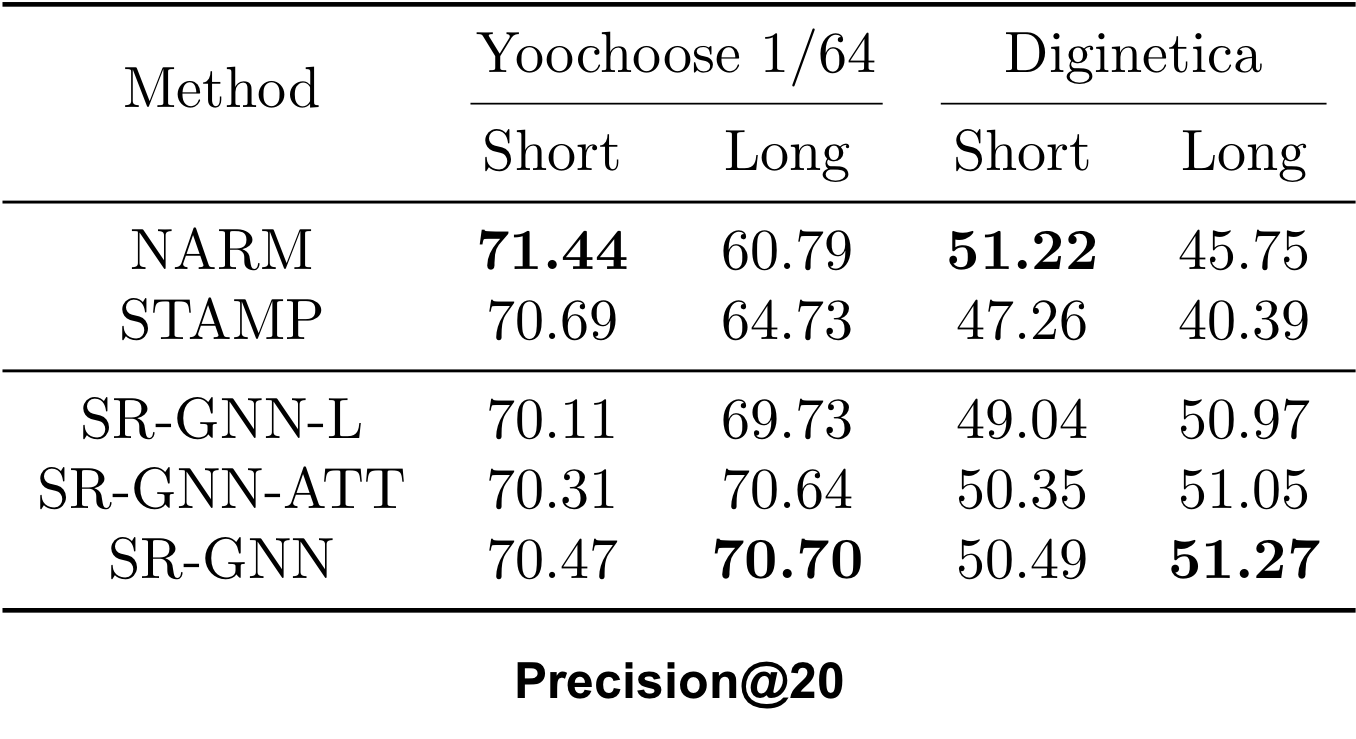
On the contrary, the performance of NARM and STAMP changes greatly in short and long groups. Although NARM achieves good performance on the short group, its performance drops quickly with the length of the sessions increasing, which is partially because RNN models have difficulty in coping with long sequences.
The variants of our method achieve promising results compared with STAMP and NARM. It is probably because that based on the learning framework of graph neural networks, our methods can attain more accurate node vectors. On such basis, the performance is stable among variants of SR-GNN, while the performance of two state-of-art methods fluctuate considerably on short and long datasets.
Please note that SR-GNN-L can also achieve good results, although this variant only uses local session embedding vectors. It is probably because that SR-GNN-L also implicitly considers the properties of the first-order and higher-order nodes in session graphs.
Concluding Remarks
-
Session-based recommendation is indispensable where users’ preference and historical records are hard to obtain.
-
We present a novel architecture for session-based recommendation that incorporates graph models into representing session sequences.
-
The proposed method not only considers the complex structure and transitions between items of session sequences, but also develops a strategy to combine long-term preferences and current interests of sessions to better predict users’ next actions.
-
Comprehensive experiments confirm that the proposed algorithm can consistently outperform other state-of-art methods.
Bibliographies
- [Hidasi et al. 2016] B. Hidasi, A. Karatzoglou, L. Baltrunas, and D. Tikk, Session-based Recommendations with Recurrent Neural Networks, in ICLR, 2016.
- [Li et al. 2016] Y. Li, D. Tarlow, M. Brockschmidt, and R. Zemel, Gated Graph Sequence Neural Networks, in ICLR, 2016.
- [Li et al. 2017] J. Li, P. Ren, Z. Chen, Z. Ren, T. Lian, and J. Ma, Neural Attentive Session-based Recommendation, in CIKM, 2017, 1419–1428.
- [Liu et al. 2018] Q. Liu, Y. Zeng, R. Mokhosi, and H. Zhang, STAMP: Short-Term Attention/Memory Priority Model for Session-based Recommendation, in KDD, 2018, 1831–1839.
- [Rendle et al. 2009] S. Rendle, C. Freudenthaler, Z. Gantner, and L. Schmidt-Thieme, BPR: Bayesian Personalized Ranking from Implicit Feedback, in UAI, 2009, 452–461.
- [Rendle et al. 2010] S. Rendle, C. Freudenthaler, and L. Schmidt-Thieme, Factorizing Personalized Markov Chains for Next-basket Recommendation, in WWW, 2010, 811–820.
- [Sarwar et al. 2001] B. Sarwar, G. Karypis, J. Konstan, and J. Riedl, Item-based collaborative filtering recommendation algorithms, in WWW, 2001, 285–295.
- [Scarselli et al. 2009] F. Scarselli, M. Gori, A. C. Tsoi, M. Hagenbuchner, and G. Monfardini, The Graph Neural Network Model, T-NN, 20 (1), 61–80, 2009.
Citation
Please cite our paper:
@inproceedings{Wu:2019ke,
title = {{Session-based Recommendation with Graph Neural Networks}},
author = {Wu, Shu and Tang, Yuyuan and Zhu, Yanqiao and Wang, Liang and Xie, Xing and Tan, Tieniu},
year = 2019,
booktitle = {Proceedings of the Twenty-Third AAAI Conference on Artificial Intelligence},
location = {Honolulu, HI, USA},
month = jul,
volume = 33,
number = 1,
pages = {346--353},
publisher = {AAAI Press},
url = {https://aaai.org/ojs/index.php/AAAI/article/view/3804},
doi = {10.1609/aaai.v33i01.3301346},
editor = {Pascal Van Hentenryck and Zhi-Hua Zhou}
}
